which pair of undefined terms is used to define a ray?

Hey there! Have you ever looked at a beam of sunlight streaming through a window or the straight path of a laser pointer? Those are real-world examples of something in geometry called a ray. In this article, we’re going to dive into the world of rays, figure out what they are, and answer a key question: which pair of undefined terms is used to define a ray? Don’t worry if geometry sounds intimidating—this is going to be clear, fun, and easy to understand, whether you’re a student, a parent, or just curious about math. Let’s get started!

What Is a Ray in Geometry?

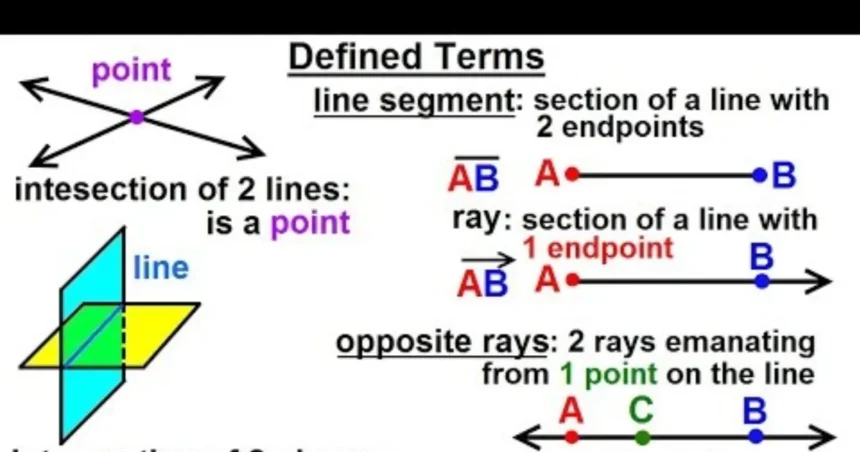
Imagine you’re holding a flashlight in a dark room. When you turn it on, the light shoots out in one direction, starting at the flashlight and going on forever. That’s a lot like a ray in geometry! A ray is a part of a line that has one starting point (called an endpoint) and extends infinitely in one direction. It’s like a line that has a beginning but no end.

To picture it:

• A line goes on forever in both directions, like an endless road.

• A line segment is a piece of a line with two endpoints, like a stick with a start and a stop.

• A ray is halfway between the two—it has one endpoint and stretches out forever in one direction, like the beam of that flashlight.

In geometry, we use specific terms to describe and define shapes, and some of these terms are so basic that we don’t even define them—we just accept them as starting points. These are called undefined terms. But before we get into those, let’s explore why rays matter and how they’re defined.

Why Are Rays Important?

Rays show up everywhere in geometry and in the real world. They help us understand:

• Angles: Two rays that share the same endpoint form an angle, like the hands of a clock at 3:00.

• Optics: Light rays help scientists study how lenses and mirrors work.

• Navigation: Rays can represent directions, like a ship sailing straight out from a port.

To define a ray properly, we need to rely on some foundational building blocks of geometry. That’s where undefined terms come in. Let’s break those down next.

What Are Undefined Terms in Geometry?

In geometry, we start with a few basic ideas that are so simple we don’t try to define them with other words. Instead, we describe them using examples or properties. These are called undefined terms, and there are three main ones:

1. Point: A point is a single location in space. It has no size, no length, no width—just a dot. Think of the tip of a pencil touching paper.

2. Line: A line is a straight path that goes on forever in both directions. It’s perfectly straight, has no thickness, and never stops. Picture a tightrope stretching to infinity.

3. Plane: A plane is a flat surface that extends forever in all directions. Imagine a perfectly smooth table that goes on forever.

These three terms are the foundation of geometry. We use them to define everything else, like rays, angles, and shapes. So, which of these undefined terms do we need to define a ray? Let’s find out!

Defining a Ray: The Key Ingredients

To define a ray, we need to describe what makes it unique: it has one endpoint and extends infinitely in one direction. Let’s think about what we need to make that happen:

• A point to mark the starting point (the endpoint).

• A line (or part of one) to show the direction that the ray extends forever.

Here’s the kicker: a ray is defined using two points on a line, where one point is the endpoint, and the other point determines the direction the ray travels. The ray starts at the first point and passes through the second point, continuing forever in that direction.

So, the pair of undefined terms used to define a ray is:

• Point (for the endpoint).

• Point (to set the direction).

Wait, did I just say point twice? Yup! A ray is defined by two points, both of which are undefined terms in geometry. Let’s dive deeper to make sure this makes sense.

How Two Points Define a Ray

Picture this: you’re standing at a starting line (let’s call it point A), and you’re looking toward a flag in the distance (point B). If you start at A and walk straight toward B, and keep going forever, you’ve just traced a ray! In geometry:

• The first point (A) is the endpoint where the ray begins.

• The second point (B) tells the ray which way to go. The ray passes through B and keeps going infinitely in that direction.

In math terms, we write a ray as ray AB (or $\overrightarrow{AB}$), where A is the endpoint, and B is a point the ray passes through. The little arrow over AB shows that the ray goes on forever in one direction.

Here’s a quick example:

• Say point A is at (0,0) on a coordinate plane, and point B is at (2,2). The ray starts at A, goes through B, and continues forever in that direction (like a diagonal line shooting out from the origin).

So, the pair of undefined terms is point and point. But why not a line or a plane? Let’s explore that next.

Why Not Line or Plane?

You might be thinking, “Doesn’t a ray look like part of a line? which pair of undefined terms is used to define a ray?” Great question! While a ray is related to a line, we don’t need the concept of a line to define a ray. Here’s why:

• A line goes on forever in both directions, but a ray only goes in one direction. To define a ray, we just need two points to set the starting point and direction.

• A plane is a flat surface, and while rays can exist in a plane, we don’t need the plane itself to define what a ray is. The plane is more about the space where the ray lives, not what makes the ray.

By using two points, we can fully describe a ray without needing to bring in lines or planes. It’s the simplest, most direct way to define it.

Table: which pair of undefined terms is used to define a ray?

To make things crystal clear, here’s a table that breaks down the undefined terms in geometry and whether they’re used to define a ray:

This table shows that only points are needed to define a ray. Two points, to be exact—one for the start and one for the direction.

Real-World Examples to Make It Stick

Let’s bring rays to life with a few examples you can picture in your everyday world:

1. Sunlight: Imagine the sun as the endpoint and a ray of light shooting out toward the Earth. That’s a ray!

2. Road Trip: Picture a road that starts at your house (the endpoint) and goes straight through a nearby town, continuing forever in that direction. That’s a ray, too.

3. Laser Pointer: When you point a laser at a wall, the beam starts at the pointer (endpoint) and travels in one direction toward the wall and beyond (in theory!).

These examples show how rays are all around us, and they’re always defined by a starting point and a direction—two points.

Common Questions About Rays

Let’s tackle some questions you might have to clear up any confusion:

Q: Can a ray have more than one endpoint?
Nope! A ray has exactly one endpoint. If it had two, it would be a line segment.

Q: What if the two points are the same?
If the two points are the same (like A and A), the ray doesn’t have a clear direction, so it’s not a valid ray. You need two distinct points.

Q: Do we ever use lines or planes to talk about rays?
Sure, rays can be on a line or in a plane, but we don’t need those terms to define what a ray is. Two points are enough.

Q: How is a ray different from an angle?
An angle is formed by two rays that share the same endpoint. So, rays are the building blocks of angles!

Why This Matters for Learning Geometry

Understanding rays and the undefined terms that define them is like learning the alphabet before you write a story. Points, lines, and planes are the basic letters of geometry, and rays are one of the first words you build with them. Once you get rays, you’re on your way to understanding angles, triangles, and all sorts of shapes.

Plus, knowing that a ray is defined by two points helps you see how simple geometry can be. You don’t need fancy tools or complicated ideas—just a couple of dots and an imagination that stretches to infinity.

A Quick Recap

So, which pair of undefined terms is used to define a ray? It’s point and point. Two points are all you need: one for the endpoint where the ray starts, and another to show the direction it goes forever. Lines and planes are important in geometry, but they’re not needed to define a ray.

To sum it up:

• A ray starts at one point and extends infinitely through another point.

• The undefined terms in geometry are point, line, and plane.

• Only points are used to define a ray, making the pair point and point.

Let’s Try It Out!

Want to test your understanding? Grab a piece of paper and try this:

1. Draw two points, label them A and B.

2. Draw a ray that starts at A and passes through B, with an arrow showing it goes on forever.

3. Now draw another point, C, and create a ray from A through C. Notice how the direction changes!

You’ve just created rays using two points each time. Pretty cool, right?

Wrapping It Up

Rays are a simple but powerful idea in geometry, and they’re defined using the most basic building blocks: points. By understanding that a ray is defined by two points—one for the endpoint and one for the direction—you’ve unlocked a key piece of geometry’s puzzle. Whether you’re imagining sunlight, laser beams, or just drawing on paper, rays are everywhere, and now you know exactly what makes them tick.